Gamut Mapping method (Nuke script example)

Discussions - ACESNext VWG – Gamut Compression/Mapping
, , ,
1

I have uploaded a Nuke script that seems to show decent results for mapping ARRI images into a target gamut. I would like to hear how it works on your footage.

The method uses a custom saturation mask derived from the target gamut to mix between white-balanced, camera native RGB values and the matrixed, less saturated values. This, of course, assumes that supersaturated (narrowband) values appear somewhat color accurate in a display-referred space. This seems to be somewhat true.

If ARRI footage that hasn’t been soft clipped (debayered into ACES) and the debayered WB values are known, it can be converted back to camera native, which this method does.

This can be used on RED footage by first debayering into RED Wide Gamut and matrixing into APO. Debayering into APO directly will clip values at APO. The conversion back to camera native is using ARRI’s math so it’s likely not accurate at all.

Since both camera RGB and the target colorspaces are linear, I assume that this method does not make these values non-linear, since it’s just mixing between the two.

Note: This method is currently configured to accept APO gamut inputs, but others can be used by changing the internal gamut conversions inside the node.

I would really like to try some of the methods described in this paper in Nuke, but do not have the skills required to convert the math to Nuke. Any takers?


-Justin Johnson

3 Likes
2

Hi Justin,

I’ll play with your script over the weekend!

Simple things doable in Nuke (and work if you are happy to manually nudge things) are along the lines of rotation to Luminance&Chrominance/Luma&Chroma space (CIE LCh, YCoCg + Polar Transformation), and then adjust the Chrominance/Chroma plane to wish.

set cut_paste_input [stack 0]
version 12.1 v1
ColorWheel {
inputs 0
format "512 512 0 0 512 512 1 square_512"
name ColorWheel
selected true
xpos 550
ypos 4
}
Colorspace {
colorspace_out CIE-LCH
name To_CIE_LCh_Colorspace
selected true
xpos 550
ypos 76
}
set N78849000 [stack 0]
Gamma {
value 0.5
name chrominance_masking_Gamma
selected true
xpos 660
ypos 100
}
push $N78849000
Multiply {
inputs 1+1
channels {-rgba.red rgba.green -rgba.blue none}
maskChannelMask rgba.green
name compression_Multiply
selected true
xpos 550
ypos 104
}
Colorspace {
colorspace_in CIE-LCH
name From_CIE_LCh_Colorspace
selected true
xpos 550
ypos 147
}
Colorspace {
colorspace_out CIE-Yxy
name To_CIE_xyY_Colorspace
selected true
xpos 550
ypos 171
}
Shuffle2 {
fromInput1 {{0} B}
fromInput2 {{0} B}
mappings "4 rgba.blue 0 2 rgba.blue 0 2 rgba.alpha 0 3 rgba.alpha 0 3 rgba.red 0 0 rgba.green 0 1 rgba.green 0 1 rgba.red 0 0"
name Axis_Reorder_Shuffle
selected true
xpos 550
ypos 209
}
PositionToPoints2 {
display textured
render_mode textured
P_channel rgb
detail 1
pointSize 4
name PositionToPoints
selected true
xpos 550
ypos 253
}

This will effectively compress and expand the gamut non-linearly, from there you can introduce some heuristics to find the compression factor and the ideal mask for the Chrominance plane. This is the hard part depending on the requirements/constraints.

This is not dependent on the linearity of your inputs but on the linearity of the transformation you apply on those inputs. For example, if you are using a non-linear mask, then your transformation is non-linear and thus most likely not exposure invariant. Whether it is a problem or not is another question :slight_smile:

We have a lot of code for that in Colour which will be easier to translate (or test directly): https://github.com/colour-science/colour/blob/develop/colour/characterisation/correction.py

What you will find is that it is not trivial to port the polynomial methods into Nuke unless somebody can share code to apply a nxn matrix to colour data efficiently. Nuke, out of the box, is limited to 3x3 via the ColorMatrix node.

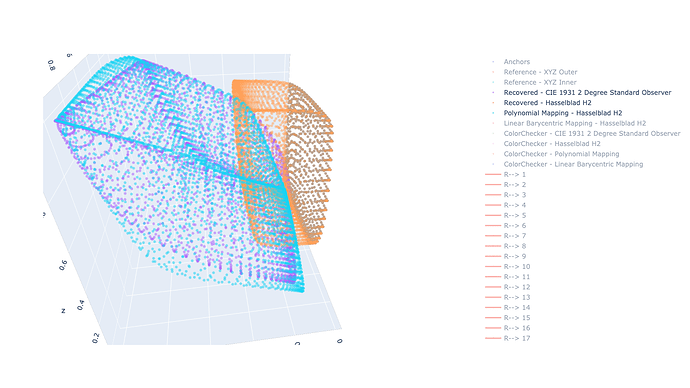
You will also find that none of the linear or polynomial methods is able to bring the data where you would like it to go. The polynomial methods will get you closer, for example, the light blue dots in that image:

newplot (3)
newplot (3)1280×720 218 KB

No cigar, unfortunately! That being said, it could be the first step to make the work easier.

Finally, polynomials are EXTREMELY dangerous, they behave quite well on the training data set, but for anything not within it, they are bound to Cosmical Explosions! One of my favorite shirt, so much that I have it :slight_smile:

image
image750×1000 106 KB

Cheers,

Thomas

2 Likes
3

It would also be subject to Abney effect given it operates on naive luma (Y’) / luminance (Y).

1 Like
4

I have updated the above script:

The results affect the in-gamut colors less than the previous version by using a Jed’s calculation for saturation and by mixing in camera native values per channel.

It seems to have minimal hue and value artifacts, but is reliant upon knowing how to transform the image values back to camera native RGB (non-matrixed) colors, and does not perfectly preserve the “confidence gamut”. Any non-linear falloff applied to the saturation masks intended to preserve these colors creates visible artifacts.

-Justin

1 Like